A recent paper (Le Lan, Dinh, 2020) [1] at the interesting-themed “I Can’t Believe it’s not Better” workshop at NeurIPS 20 asserts the following:
Principle: “In an infinite data and capacity setting, the result of an anomaly detection [AD] method should be invariant to any continuous invertible reparametrization.”
In other words, the status of an “anomaly” in the observed data is a latent property associated with each outcome, preserved across any choice of invertible reparameterization - the coordinate system used to define the AD method does not carry any information. Whether or not you consider this principle realistic will depend on your definition of an anomaly.
Preliminaries
The task of anomaly detection is to partition the input space of the observed data $\mathcal{X}$ into the disjoint ‘inlier’ \(\mathcal{X}_{in}\) and ‘anomalous’ \(\mathcal{A}\) sets such that \(\mathcal{X} = \mathcal{X}_{in} \, \bigcup \, \mathcal{A}\). The main contention of the paper is that the status of anomaly-or-not is inherently attached to outcomes $\omega \in \Omega$ in some sample space, and that this status should remain invariant with respect to the choice of random variable $X: \omega \rightarrow \mathcal{X}$ mapping $\omega$ to the observed data. The authors argue that any invertible map $f$ should not affect the anomaly-or-not status of $\omega$ - that is the observation $x = X(\omega)$ before reparameterization and the observation $f(x) = f \circ X(\omega)$ after reparameterization should be classified identically by an ideal anomaly detection algorithm.
One general but non-constructive way of defining the set of anomalies $\mathcal{A}$ is as a set of outcomes $\omega$ of low probability mass. That is, \(\mathbb{P}\left(X(\omega) \in \mathcal{A}\right) \leq \alpha\) for some small $\alpha$. We know any invertible transformation $f$ should be volume-preserving:
\[\begin{align*} \int_{x \in \mathcal{A}} dx \, p_X(x) &= \int_{y \in f(\mathcal{A})} dy \, p_{f(X)}(y) \\ \implies \mathbb{P}\left(X(\omega) \in \mathcal{A}\right) &= \mathbb{P}\left(f \circ X(\omega) \in f\left(\mathcal{A}\right)\right). \end{align*}\]So this provides a reparameterization-invariant definition of the set of anomalies, but gives no mechanism to construct $\mathcal{A}$.
Reparameterization
One natural way of defining this subset is using the ‘true’ probability density \(p_X^{*}\) over the observed data:
\[\begin{equation} \label{eq:level_set} \mathcal{A} = \{ x \in \mathcal{X} \; \vert \; p_X^{*}(x) \leq \lambda \} \end{equation}\]That is, anomalous points are points whose density falls below the threshold $\lambda$ chosen such that $\mathcal{A}$ covers a region of low probability mass. To practically identify points $x \in \mathcal{A}$, one may use generative models which approximate \(p_X^{*}\) by some parametric model $p_X^{(\theta)}$. To avoid issues with model mis-specification, the paper works in the ‘infinite data/capacity’ setting, where the learnt density matches the ground truth exactly, \(p_X^{(\theta)} = p_X^{*}\).
Defining anomalies this way, as points of low probability density fails to satisfy the invariance principle, as these methods bind the definition of $\mathcal{A}$ to a particular choice of representation. From change of variables under the invertible map $f$ we know:
\[\begin{equation} \label{eq:cov} p_{f(X)}(f(x)) = p_X(x) \cdot \left\vert \textsf{det}\left( J_f(x) \right) \right\vert^{-1}. \end{equation}\]Where $J_f$ denotes the Jacobian of the transformation. Put another way, the density $\lambda$-level sets (Eq. $\ref{eq:level_set}$) are not necessarily preserved under an invertible transformation, and the anomaly/not-anomaly status becomes dependent on the parameterization. The figure below provides a slightly contrived example of how an invertible mapping changes the density associated with each point in the original representation.
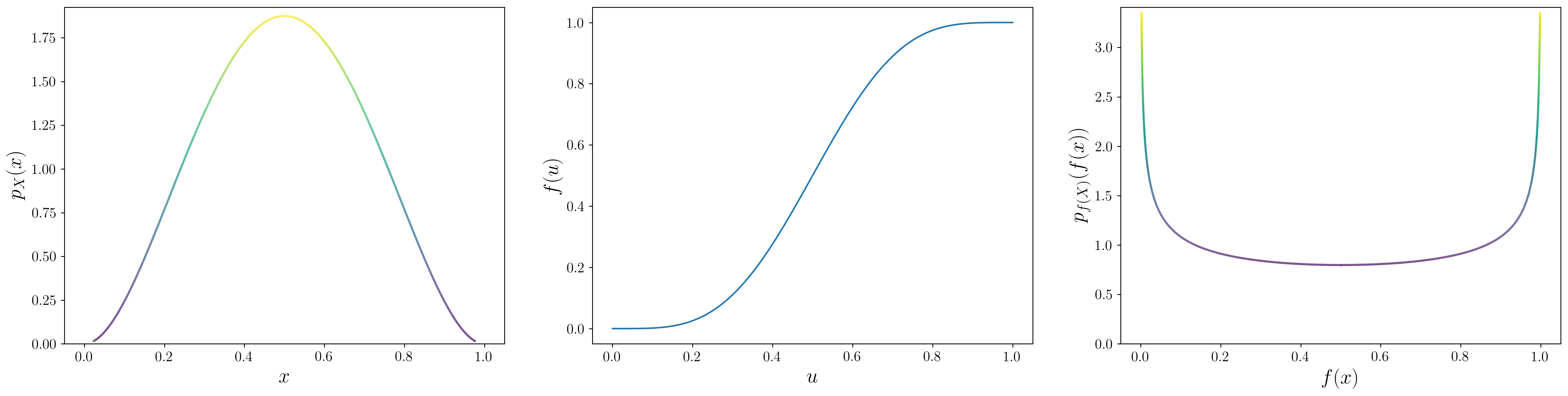
One can also subject $X$ to some sort of multivariate probability integral transform \(f: \mathcal{X} \rightarrow [0,1]^D\) such that $f(X)$ is uniformly distributed on the hypercube. Density-based anomaly detection in this parameterization cannot draw any useful conclusions here as $p_{f(X)}(f(x)) = 1 \, \forall \, x \in \mathcal{X}$. The authors further proceed to show that, given knowledge of the true density $p_X^*$, it is possible (if impractical) to find a continuous mapping that assigns an arbitrary density to each datapoint $x \in \mathcal{X}$, which means the performance of any density-based anomaly detection method can be made arbitrarily bad, even in the infinite-capacity limit.
Invariants
One way of defining a quantity which is invariant across any reparameterization induced by an invertible map is as a ratio of densities, or more generally, something which looks like the expectation of a ratio. Given two densities $p_X, q_X$, some function which transforms as a density $r(x)$ under reparameterization, and some integrable function $g$, this can be defined as:
\[\begin{equation} \Phi(p, q) = \int dx \, r(x) \, g\left(\frac{p_X(x)}{q_X(x)}\right) \end{equation}\]Changing coordinates under a invertible map $x’ = f(x)$ doesn’t change the value of $\Phi$:
\[\begin{align*} \Phi(p', q') &= \int \left[ dx \left\vert \textsf{det}(J_f(x))\right\vert \right] \, \left[ \frac{r \circ f^{-1}(x')}{\left\vert \textsf{det}(J_f(x))\right\vert } \right] g\left(\frac{p_X \circ f^{-1}(x')}{q_X \circ f^{-1}(x')} \cdot \frac{\left\vert \textsf{det}(J_f(x))\right\vert}{\left\vert \textsf{det}(J_f(x))\right\vert}\right) \\ &= \Phi(p,q) \end{align*}\]Where we used the fact that the probability density transforms according to Eq. \ref{eq:cov} under change of coordinates. Here $p_X$ can be taken to be the model density, and $q_X$ a ‘reference’ distribution on which anomalous events should exhibit qualitatively different behaviour from $p_X$. If we choose $r(x) = q_X(x)$ and $g$ convex, then $\Phi$ belongs to the family of $f$-divergences. This kind of ‘ratio’ figure of merit is used widely in the AD literature ([3], [4]), although not (explicitly) motivated by the invariance principle, to the best of my knowledge.
Symmetries
The invariance principle put forward by the authors may be too strong a condition for useful anomaly detection methods. Forcing your algorithm to output predictions invariant w.r.t. arbitrary invertible reparameterization seems too restrictive, and it’s not clear what benefit you could expect from this over a method that works well in certain representations but gets confused in others.
A problem-dependent relaxation of the principle may offer a useful starting point. In situations where we have knowledge of the symmetries the problem should satisfy, it would likely be helpful to directly inject this domain knowledge into our algorithm, such that the probability density is invariant to a problem-dependent subclass of invertible reparameterizations. Formally, if we know the underlying symmetry group $\mathcal{G}$ and have some kind of representation of the group action $g$, $\rho(g) \in \mathcal{G}$, $\rho(g): \mathcal{X} \rightarrow \mathcal{X}$, the density of the transformed input should be left unchanged from the original input.
\[\begin{equation} p_{\theta}(\rho(g) \cdot x) = p_{\theta}(x) \; \forall \; x \in \mathcal{X}, g \in \mathcal{G} \end{equation}\]For instance, for modelling many-body systems which exhibit rotational and translational symmetry about the center of mass, our model should recognize that the particle configuration after a rotation/translation is not arbitrarily different from the original configuration, and should be identified with the original in terms of density. Here the symmetry group $\mathcal{G}$ would be the 3-dimensional special Euclidean group SE(3), and the $\rho(g)$ would be $4 \times 4$ rotation/translation matrices.

I’m not sure if this will outperform just throwing the deepest generative model you have at the problem, but this may help bias our methods toward learning useful representations (not the group kind) so that we may successfully apply Eq. $(\ref{eq:level_set})$ or something similar for anomaly detection. This line of thinking has been investigated in [5] in the context of generative models for field configurations in lattice QCD with SU(N) gauge symmetry.
Discussion
Approaches which identify anomalies via Eq. $\ref{eq:level_set}$, or related methods such as those based on weak typicality [2], cannot satisfy the above invariance principle - it is possible to manipulate the information contained within the density in an adversarial manner such that the resulting anomaly detection method performs poorly.
However, we know that existing density-based anomaly detection methods are commonplace and relatively successful. Let us make the simplifying assumption that the representations we are interested in can be obtained via invertible mappings. Then exist a large range of representations which are both easily learnable and separate inliers from outliers well through their learned densities. The natural question is which choice of random variable $X$ leads to the best anomaly detection performance? This cuts to the heart of how to define an anomaly. It seems natural to define anomalies using the original input representation. That is, using Eq. $\ref{eq:level_set}$, where \(p_X^*\) is the true data-generating distribution of the input. From this perspective, in the infinite data/capacity limit, estimating \(p_X^*\) would be guaranteed to succeed at detecting every anomaly.
However, in the real, finite-capacity world, there is no guarantee that this would be ideal. Much of the success of deep learning is predicated on representation learning; downstream tasks typically operate on a highly processed function of the original representation. The same may hold for anomaly detection - it is likely there exists an alternative representation where anomalies are easier to separate from non-anomalies. Furthermore, according to the manifold hypothesis, the effective dimensionality of the data may be much smaller than the ambient dimensionality, and estimating the density in the original given representation is likely to be inefficient. For high-dimensional human-perceptual data such as images/audio, it’s probably best to search for some alternate representation of the data which abstracts away irrelevant detail prior to density estimation. For scientific data, it may be desirable to find a representation which illuminates the physical origins of the data. For example, using graph-learned representations for decay chains in high-energy physics, or molecular dynamics.
Alternatively, if we consider anomaly status to be a latent variable attached to each outcome, as the paper suggests, then the problem becomes analogous to binary classification. Using this definition of anomaly, the invariance principle becomes more reasonable, but still a very strong assumption. In this case, using the original input data representation is not guaranteed to be ideal, even in the infinite-capacity setting. This is because it is not possible to determine whether a point is drawn from one of two distributions with overlapping support, and there may exist an alternate parameterization in which the anomaly and non-anomaly distributions are better separated than the original input representation.
Summary/TL;DR
- Density based methods which rely on Eq. (\ref{eq:level_set}) for anomaly detection are inherently coupled to a particular choice of representation.
- The original input representation is not necessarily the ideal space to measure likelihoods in for finite-capacity models.
- Problem-agnostic anomaly detection methods can be misled by reparameterization and a useful definition of anomalies is likely to be domain-specific.
- The original invariance statement up top may be too strong; instead requiring your AD method to be invariant to the underlying symmetries of your problem may be a more achievable and useful principle. This will be problem-specific and again requires us to explicitly build domain knowledge into the AD method.
References
[1] Charline Le Lan and Laurent Dinh. “Perfect density models cannot guarantee anomaly detection.”, I Can’t Believe it’s not Better Workshop, NeurIPS 2020.
[2] Eric Nalisnick, Akihiro Matsukawa, Yee Whye Teh, Balaji Lakshminarayanan. “Detecting Out-of-Distribution Inputs to Deep Generative Models Using Typicality.”, arXiv:1906.02994 (2019).
[3] Serrà, Joan, et al. “Input complexity and out-of-distribution detection with likelihood-based generative models.” arXiv preprint arXiv:1909.11480 (2019).
[4] Nachman, Benjamin, and David Shih. “Anomaly detection with density estimation.” Physical Review D 101.7 (2020): 075042.
[5] Boyda, Denis, et al. “Sampling using SU(N) gauge equivariant flows.” arXiv preprint arXiv:2008.05456 (2020).
